배운 내용
- KMeans.fit()
- make_blobs() & np.unique()
- KMeans.fit_predict()
- KMeans.cluster_centers_
- sihouette_samples()
- silhouette_score()
- DataFrame.groupby()
- MeanShift
- MeanShift.fit_predict()
- sklearn.cluster.estimate_bandwidth
- MeanShift.cluster_centers_
- sklearn.mixture.GaussianMixture
- GaussianMixture.fit()
- GaussianMixture.predict()
- sklearn.cluster.DBSCAN
본문
K-평균은 군집화(Clustering)에서 가장 일반적으로 사용되는 알고리즘입니다. K-평균은 군집 중심점(Centroid)라는 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택하는 군집화 기법입니다.

시작은 원하는 군집(그룹)의 갯수만큼 임의의 위치로 Centroid를 만듭니다. 그 후 각 군집에 속하는 데이터들의 평균 지점으로 Centroid를 옮기고, 다시 그 Centroid에 가까운 데이터들을 그 군집으로 소속시킵니다. 다시 Centroid를 각 군집에 속한 데이터의 평균 지점으로 옮기고, 이 것을 계속 반복하다가 Centroid를 데이터의 평균 지점으로 옮겼을 때 데이터들이 군집의 변화가 없다면, 군집화를 완료합니다.
K-평균 알고리즘의 장점
- 일반적인 군집화에서 가장 많이 활용되는 알고리즘입니다.
- 알고리즘이 쉽고 간결합니다.
K-평균 알고리즘의 단점
- 거리 기반 알고리즘으로 속성의 개수(X, Y 등 축)가 많을 때 군집화 정확도가 떨어집니다. 이를 위해 PCA로 차원 감소를 적용하기도 합니다.
- 반복을 수행하는데, 반복 횟수가 많을 경우 수행 시간이 느려집니다.
- 몇 개의 군집(cluster)을 선택해야할 지 가이드하기 어렵습니다.
사이킷런 KMeans 클래스 소개
사이킷런 패키지는 K-평균을 구현하기 위해 KMeans 클래스를 제공합니다.
class sklearn.cluster.KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, \
verbose=0, random_state=None, copy_x=True, algorithm='auto')여기서 중요한 파라미터는 아래와 같습니다.
- n_clusters: 이는 군집화할 개수, 즉 군집 중심점의 개수를 의미합니다.
- init: 초기에 군집 중심점 좌표를 설정할 방식을 만하며, 임의로 설정하지 않고 일반적으로 'k-means++'를 사용합니다.
- max_iter: 최대 반복 횟수이며, 이 횟수 이전에 모든 데이터의 중심점 이동이 없으면 종료합니다. default는 300입니다.
KMeans는 사이킷런의 비지도학습 클래스와 마찬가지로 fit(데이터 세트) 또는 fit_transform(데이터 세트) 메서드를 이용해 수행하면 군집화 수행이 완료됩니다.
KMeans 객체는 군집화와 관련된 주요 속성을 통해 아래와 같이 알려줍니다.
- labels_: 각 데이터 포인트가 속한 군집 중심점 레이블(각 데이터가 속한 군집)
- cluster_centers_: 각 군집 중심점 좌표(Shape는 [군집 개수, 피처 개수]). 이를 이용하면 군집 중심점 좌표가 어디인지 시각화할 수 있습니다.
K-평균을 이용한 붓꽃 데이터 세트 군집화
붓꽃 데이터를 이용해 꽃받침, 꽃잎의 너비와 길이에 따라 각 데이터의 군집화가 어떻게 결정되는지 확인해보고, 이를 분류값과 비교해보겠습니다.
from sklearn.preprocessing import scale
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
iris = load_iris()
# 더 편리한 데이터 핸들링을 위해 DataFrame으로 변환
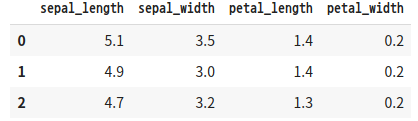
irisDF = pd.DataFrame(data=iris.data, columns=['sepal_length', 'sepal_width',\
'petal_length', 'petal_width'])
irisDF.head(3)
'''
결과1
'''
KMeans.fit()
붓꽃 데이터 세트를 3개 그룹으로 군집화해보겠습니다.
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=0)
kmeans.fit(irisDF)fit()을 수행해 irisDF 데이터에 대한 군집화 수행 결과가 kmeans 객체 변수로 반환됐습니다. labels_ 속성값을 출력해보겠습니다.
print(kmeans.labels_)
'''
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 2 2 2 0 2 2 2 2
2 2 0 0 2 2 2 2 0 2 0 2 0 2 2 0 0 2 2 2 2 2 0 2 2 2 2 0 2 2 2 0 2 2 2 0 2
2 0]
'''실제 붓꽃 품종 분류값과 군집화(clustering)한 값이 차이가 얼마나 되는지 group by 연산을 통해 비교해보겠습니다.
irisDF['target'] = iris.target
irisDF['cluster'] = kmeans.labels_
iris_result = irisDF.groupby(['target', 'cluster'])['sepal_length'].count()
print(iris_result)
'''
target cluster
0 1 50
1 0 48
2 2
2 0 14
2 36
'''target 분류값이 0을 1번 군집으로 모두 잘 그루핑했습니다. target 1 값 이터는 대부분 0번 군집으로 잘 그루핑 했습니다. 그런데, Target 2 값의 경우 50건 중 36건만 2번 군집으로 그루핑했음을 알 수 있습니다.
이번엔 붓꽃 데이터 세트의 군집화를 시각화해보겠습니다. 2차원 평면상으로 나타내기엔 피처가 4개이므로 PCA를 통해 2개로 차원축소한 뒤 X 좌표 ,Y 좌표로 개별 데이터를 표현하도록 하겠습니다.
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca_transformed = pca.fit_transform(iris.data)
# pca_component_1에 투영한 값
irisDF['pca_X'] = pca_transformed[:, 0]
# pca_component_2에 투영한 값
irisDF['pca_Y'] = pca_transformed[:, 1]
irisDF.head(3)
'''
결과2
'''
cluster 0은 마커'o', cluster 1은 마커's', cluster 2는 마커'^'로 표현하겠습니다. matplotlib scatter는 서로 다른 마커를 한 번에 표현할 수 없으므로 마커 별로 별도의 산점도를 수행합니다.
# 군집값이 0, 1, 2인 경우마다 별도의 인덱스로 추출
marker0_ind = irisDF[irisDF['cluster']==0].index
marker1_ind = irisDF[irisDF['cluster']==1].index
marker2_ind = irisDF[irisDF['cluster']==2].index
# 군집값 0, 1, 2에 해당하는 인덱스로 각 군집 레벨의 pca_x, pca_y 값 추출
# o, s, ^로 마커 표시
plt.scatter(x=irisDF.loc[marker0_ind, 'pca_X'], y=irisDF.loc[marker0_ind, 'pca_Y'], marker='o')
plt.scatter(x=irisDF.loc[marker1_ind, 'pca_X'], y=irisDF.loc[marker1_ind, 'pca_Y'], marker='s')
plt.scatter(x=irisDF.loc[marker2_ind, 'pca_X'], y=irisDF.loc[marker2_ind, 'pca_Y'], marker='^')
plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.title('3 Clusters Visualization by 2 PCA Components')
plt.show()
'''
결과3
'''
cluster 1(네모)는 cluster 0(동그라미), cluster 2(세모)와 달리 명확히 구분됐지만, 동그라미, 세모의 경우는 상당 수준 분리돼있지만 네모처럼 명확히 분리되지는 않았습니다. 이는 cluster 0과 2의 경우 피처의 위치 자체가 명확히 분리되기 어려운 부분이 존재합니다.
군집화 알고리즘 테스트를 위한 데이터 생성
사이킷런은 군집화용 데이터 생성기를 제공합니다. 대표적으로 make_blobs()와 make_classification() API가 있습니다. 두 API는 비슷하게 여러 개의 클래스에 해당하는 데이터 세트를 만드는데, 하나의 클래스에 여러 개의 군집이 분포될 수 있게 데이터를 생성할 수 있습니다.
두 API 중 어느 것을 써도 상관은 없지만, make_blobs()는 개별 군집의 중심점과 표준 편차 제어 기능이 있습니다. make_classification()은 노이즈를 포함한 데이터를 생성할 수 있습니다. 둘 다 분류용 데이터 생성기로도 사용 가능합니다. 이 외에 make_circle(), make_moon() API는 중심 기반 군집화로 해결하기 어려운 데이터 세트를 만드는 데 사용됩니다.
make_blobs()을 호출하면 피처 데이터 세트와 타깃 데이터 세트가 Tuple(튜플)로 반환됩니다. make_blobs의 호출 파라미터는 다음과 같습니다.
- n_samples: 생성할 총 데이터의 개수입니다. default=100
- n_features: 데이터의 피처 개수입니다. 시각화를 목표로 할 경우 2개로 설정하고, 첫 번째 피처는 x좌표, 두 번째 피처는 y좌표상에 표현합니다.
- centers: init 값, 예를 들어 3으로 설정하면 군집의 개수를 나타냅니다. 그렇지 않고 ndarray 형태로 표현하면 개별 군집 중심점의 좌표를 의미합니다.
- cluster_std: 생성될 군집 데이터의 표준 편차를 의미합니다. 0.8로 지정하면 모든 군집 내에서 데이터가 표준편차 0.8을 가지고, [0.8, 1.2, 0.6]과 같은 리스트로 표현하면 군집 1은 표준편차를 0.8 .. 군집3은 표준편차를 0.6으로 가지게 됩니다.
make_blobs() & np.unique()
예제를 통해 군집용 데이터 세트를 만들어보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
%matplotlib inline
X, y = make_blobs(n_samples=200, n_features=2, centers=3,\
cluster_std=0.8, random_state=0)
print(X.shape, y.shape)
# y target값의 분포를 확인
unique, counts = np.unique(y, return_counts=True)
print(unique, counts)
'''
(200, 2) (200,)
[0 1 2] [67 67 66]
'''np.unique()는 데이터의 값에 갯수를 세주는 모양이다. 만든 데이터들을 DataFrame으로 만들겠습니다.
import pandas as pd
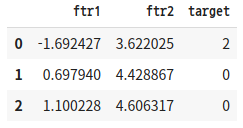
clusterDF = pd.DataFrame(data=X, columns=['ftr1', 'ftr2'])
clusterDF['target'] = y
clusterDF.head(3)
'''
결과4
'''
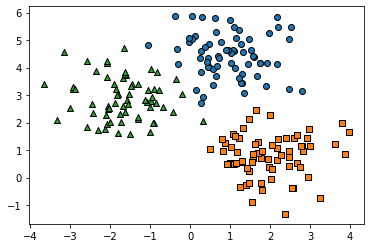
이 데이터를 앞선 붓꽃 데이터 세트처럼 산점도로 시각화해 분포도를 확인해보겠습니다.
target_list = np.unique(y)
# 각 타깃별 산점도의 마커값.
markers=['o','s','^','P','D','H','x']
# 3개의 군집 영역으로 구분한 데이터 세트를 생성했으므로 target_list는 [0, 1, 2]
# target==0, target==1, target==2로 scatter plot을 marker 별로 생성.
for target in target_list:
target_cluster = clusterDF[clusterDF['target']==target]
plt.scatter(x=target_cluster['ftr1'], y=target_cluster['ftr2'], edgecolor='k',\
marker=markers[target])
plt.show()
'''
결과5
'''
KMeans.fit_predict() & KMeans.cluster_centers_
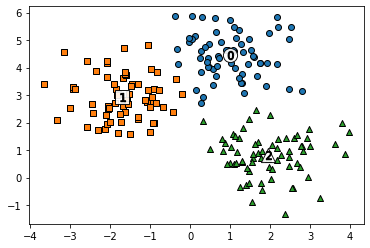
군집용 데이터에 KMeans 군집화를 수행해보겠습니다. KMean.fit_predict()를 통해 구현해보겠습니다. KMeans.cluster_centers_ 속성은 군집의 중심 위치 좌표를 나타냅니다.
# KMeans 객체를 이용해 X 데이터를 K-Means 클러스터링 수행
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=200, random_state=0)
cluster_labels = kmeans.fit_predict(X)
clusterDF['kmeans_label'] = cluster_labels
# cluster_centers_는 개별 클래스터의 중심 위치 좌표 시각화를 위해 추축ㄹ
centers = kmeans.cluster_centers_
unique_labels = np.unique(cluster_labels)
markers = ['o', 's', '^', 'P', 'D', 'H', 'x']
# 군집화된 label 유형 별로 iteration하면서 marker 별로 scatter plot 수행.
for label in unique_labels:
label_cluster = clusterDF[clusterDF['kmeans_label']==label]
center_x_y = centers[label]
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], edgecolor='k',\
marker=markers[label])
# 군집 별 중심 위치 좌표 시각화
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=200, color='white',\
alpha=0.9, edgecolor='k', marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k',\
edgecolor='k', marker='$%d$' % label)
'''
결과6
'''
print(clusterDF.groupby('target')['kmeans_label'].value_counts())
'''
target kmeans_label
0 0 66
1 1
1 2 67
2 1 65
2 1
Name: kmeans_label, dtype: int64
'''거의 대부분 군집이 잘 매핑됐습니다.
make_blobs()는 cluster_std 파라미터로 데이터 분포도를 조절합니다. cluster_std가 클 수록 군집 중심에서 데이터가 퍼져있습니다. 반대로 작을 수록 군집 중심에 데이터가 모여있습니다.
군집 평가(Cluster Evalutaion)
대부분의 군집화 데이터 세트는 정답을 비교할 타깃 레이블을 가지고 있지 않습니다. 군집화는 분류(Classification)와 유사해 보일 수 있으나 성격이 많이 다릅니다. 데이터 내에 숨어 있는 별도의 그룹을 찾아서 의미를 부여하거나 동일한 분류값에 속하더라도 그 안에서 더 세분화된 군집화를 추구하거나 서로 다른 분류값의 데이터도 더 넓은 군집화 레벨화 등의 영역을 가지고 있습니다.
군집화와 같이 비지도학습의 특성상 어떠한 지표라도 정확히 성능을 평가하기는 어렵지만, 대표적인 방법으로 실루엣 분석을 이용합니다.
실루엣 분석의 개요
군집화 평가 방법으로 실루엣 분석(silhouette analysis)이 있습니다. 실루엣 분석은 각 군집 간의 거리가 얼마나 효율적으로 분리돼있는지를 나타냅니다. 군집화가 잘 돼있다는 것은 다른 군집끼리는 멀고, 같은 군집끼리의 데이터는 가깝게 뭉쳐있다는 뜻입니다.
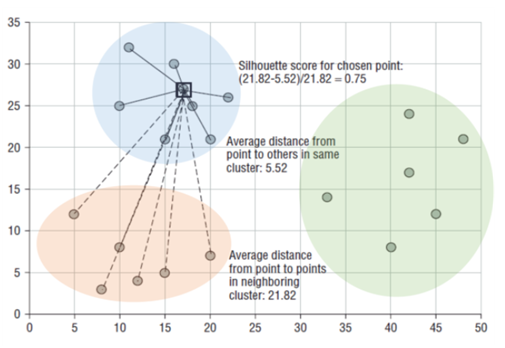
실루엣 계수는 다음과 같이 정의됩니다. a(i)는 파란 원에 속한 데이터들 속 검정색으로 표시된 점인 i번째 데이터와 자신이 속한 군집(파란 원)의 데이터와의 평균 거리입니다. b(i)는 검정색으로 표시된 점인 i번째 데이터와 가장 가까운 다른 군집(빨간 타원)에 속한 데이터와의 평균 거리입니다.
$$s\left(i\right)\ =\ \frac{b\left(i\right)\ -\ a\left(i\right)}{\max \left(a\left(i\right),\ b\left(i\right)\right)}$$
실루엣 계수 s(i)는 -1 ~ 1의 값을 가지는데, 1로 가까워질 수록 근처의 군집과 멀리 떨어져 있다는 것이고 0으로 가까워질 수록 근처의 군집과 가까워진다는 의미입니다. -값은 아예 다른 군집에 데이터 포인트가 할당됐음을 뜻합니다.
사이킷런에서 제공하는 실루엣 분석 메서드입니다.
- sklearn.metrics.silhouette_samples(X, labels, metric='euclidean', **kwds): X에 피처 데이터 세트, labels에 X 데이터 세트가 속한 군집 레이블 값을 입력하면 각 포인트의 실루엣 계수를 계산해 반환합니다.
- sklearn.metrics.silhouette_score(X, labels, metrics='euclidean', sample_size=None, **kwds): X는 피처 데이터 세트, y는 X가 속한 군집 레이블 값을 입력하면 전체 데이터의 실루엣 계수값을 평균해 반환합니다. 즉 np.mean(silhouette_samples())입니다. 이 값이 높을 수록 군집화가 잘 됐다고 어느 정도 판단할 수 있습니다,
좋은 군집화가 되려면 다음 기준을 만족해야합니다.
- 전체 실루엣 계수의 평균값, sklearn.metrics.silhouette_score() 값이 0~1 사이의 값을 갖고, 1에 가까울 수록 좋습니다.
- 하지만 전체 실루엣 계수의 평균값과 더불어 개별 군집의 평균값의 편차가 크지 않아야합니다. 즉, 특정 군집의 실루엣 계수 평균값만 유난히 높고 다른 군집들의 실루엣 계수 평균값이 낮으면 좋은 군집화 조건이 아닙니다.
붓꽃 데이터 세트를 이용한 군집 평가
sihouette_samples() & silhouette_score()
from sklearn.preprocessing import scale
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
# 실루엣 분석 평가 지표값을 구하기 위한 API 추가
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
iris = load_iris()
feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
irisDF = pd.DataFrame(data=iris.data, columns=feature_names)
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=0).fit(irisDF)
irisDF['cluster'] = kmeans.labels_
# iris의 모든 개별 데이터에 실루엣 계수값을 구함.
score_samples = silhouette_samples(iris.data, irisDF['cluster'])
print('silhouette_samples() return 값의 shape', score_samples.shape)
# irisDF에 실루엣 계수 칼럼 추가
irisDF['silhouette_coeff'] = score_samples
# 모든 데이터의 평균 실루엣 계수값을 구함.
average_score = silhouette_score(iris.data, irisDF['cluster'])
print('붓꽃 데이터 세트 Silhouette Analysis Score:{0:.3f}'.format(average_score))
irisDF.head(3)
'''
silhouette_samples() return 값의 shape (150,)
붓꽃 데이터 세트 Silhouette Analysis Score:0.553
'''
'''
결과1
'''
평균 실루엣 계수값은 0.553인데, cluster 1의 실루엣 계수는 0.8 이상 높은 실루엣 계수를 가지고 있습니다. 이는 1번 군집이 아닌 다른 군집의 경우 실루엣 계수 값이 평균보다 낮다는 것을 의미합니다. DataFrame에서 군집 칼럼 별로 group by하여 silhouette_coeff 칼럼의 평균값을 구하면 됩니다.
DataFrame.groupby()
irisDF.groupby('cluster')['silhouette_coeff'].mean()
'''
cluster
0 0.417320
1 0.798140
2 0.451105
Name: silhouette_coeff, dtype: float64
'''군집 0, 2는 상대적으로 실루엣 계수가 평균값보다 낮습니다.
군집별 평균 실루엣 계수의 시각화를 통한 군집 개수 최적화 방법
개별 군집별로 적당히 분리된 거리를 유지하면서도 군집 내의 데이터가 서로 뭉쳐 있는 경우에 K-평균의 적절한 군집 개수가 설정됐다고 판단할 수 있습니다.
사이킷런 문서 중 http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html에 이러한 방법을 시각적으로 지원해주는 좋은 예제가 있습니다. 저 문서에서 군집별 평균 실루엣 계수값을 구하는 부분만 별도의 함수로 만들어서 이를 시각화해보겠습니다.
### 여러개의 클러스터링 갯수를 List로 입력 받아 각각의 실루엣 계수를 면적으로 시각화한 함수 작성
def visualize_silhouette(cluster_lists, X_features):
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import math
# 입력값으로 클러스터링 갯수들을 리스트로 받아서, 각 갯수별로 클러스터링을 적용하고 실루엣 개수를 구함
n_cols = len(cluster_lists)
# plt.subplots()으로 리스트에 기재된 클러스터링 수만큼의 sub figures를 가지는 axs 생성
fig, axs = plt.subplots(figsize=(4*n_cols, 4), nrows=1, ncols=n_cols)
# 리스트에 기재된 클러스터링 갯수들을 차례로 iteration 수행하면서 실루엣 개수 시각화
for ind, n_cluster in enumerate(cluster_lists):
# KMeans 클러스터링 수행하고, 실루엣 스코어와 개별 데이터의 실루엣 값 계산.
clusterer = KMeans(n_clusters = n_cluster, max_iter=500, random_state=0)
cluster_labels = clusterer.fit_predict(X_features)
sil_avg = silhouette_score(X_features, cluster_labels)
sil_values = silhouette_samples(X_features, cluster_labels)
y_lower = 10
axs[ind].set_title('Number of Cluster : '+ str(n_cluster)+'\n' \
'Silhouette Score :' + str(round(sil_avg,3)) )
axs[ind].set_xlabel("The silhouette coefficient values")
axs[ind].set_ylabel("Cluster label")
axs[ind].set_xlim([-0.1, 1])
axs[ind].set_ylim([0, len(X_features) + (n_cluster + 1) * 10])
axs[ind].set_yticks([]) # Clear the yaxis labels / ticks
axs[ind].set_xticks([0, 0.2, 0.4, 0.6, 0.8, 1])
# 클러스터링 갯수별로 fill_betweenx( )형태의 막대 그래프 표현.
for i in range(n_cluster):
ith_cluster_sil_values = sil_values[cluster_labels==i]
ith_cluster_sil_values.sort()
size_cluster_i = ith_cluster_sil_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_cluster)
axs[ind].fill_betweenx(np.arange(y_lower, y_upper), 0, ith_cluster_sil_values, \
facecolor=color, edgecolor=color, alpha=0.7)
axs[ind].text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
axs[ind].axvline(x=sil_avg, color="red", linestyle="--")visualize_silhouette()함수는 군집 개수를 변화시키면서 K-평균 군집을 수행했을 때 개별 군집별 평균 실루엣 계수 값을 시각화해서 군집의 개수를 정하는 데 도움을 줍니다. 첫 번째 파라미터로 클러스터의 개수 후보를 리스트로 입력하고, 두 번째 파라미터로는 피처 데이터 세트를 입력합니다.
make_blobs()를 통해 2차원 데이터 세트를 만들고 K-평균으로 군집화할 때 2개, 3개, 4개, 5개 중 최적의 군집 개수를 시각화로 알아보겠습니다.
# make_blobs를 통해 군집화를 위한 4개의 군집 중심의 500개 2차원 데이터 세트 생성
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=500, n_features=2, centers=4, cluster_std=1,\
center_box=(-10.0, 10.0), shuffle=True, random_state=1)
# 군집 개수가 2개, 3개, 4개, 5개일 때의 군집별 실루엣 계수 평균값을 시각화
visualize_silhouette([2, 3, 4, 5], X)
'''
결과2
'''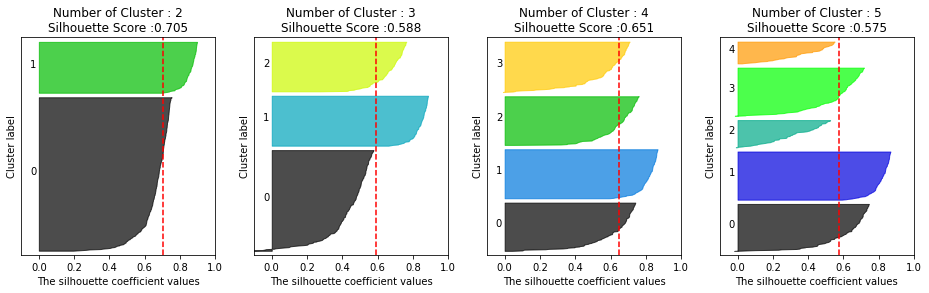
데이터 생성시 군집을 4개로 만든 것과 결과가 일치합니다. 군집 4개를 생성할 시 대부분의 군집 속 데이터가 평균 실루엣 계수를 넘고, 군집 간에도 실루엣 계수가 크게 차이나지 않습니다.
이번엔 붓꽃 데이터에 visualize_silhouette()함수를 적용해보겠습니다.
from sklearn.datasets import load_iris
iris = load_iris()
visualize_silhouette([2, 3, 4, 5], iris.data)
'''
결과3
'''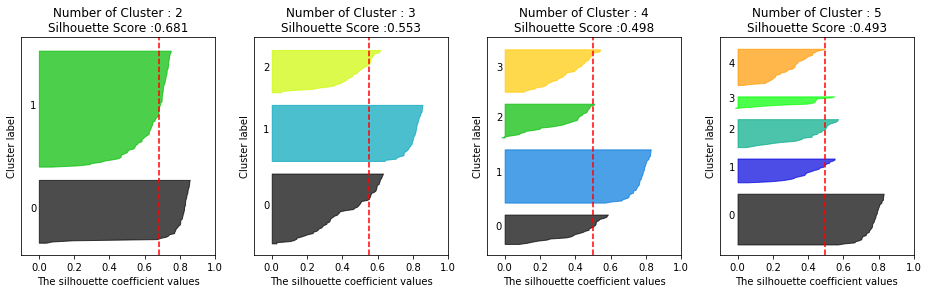
결과3을 보아 군집을 2개로 설정하는 것이 가장 좋아 보입니다.
이렇게 실루엣 계수를 통한 K-평균 군집 평가 방법을 소개했는데, 실루엣 계수는 각 데이터 별로 다른 데이터와의 거리를 반복적으로 계산해야하므로 데이터 양이 늘어나면 수행 시간이 크게 늘어납니다. 특히 몇 만건 이상의 데이터에 대해 사이킷런의 실루엣 계수 평가 API를 개인용 PC에서 수행할 경우 메모리 부족 등의 에러가 발생할 수 있습니다. 이 경우 군집 별로 임의의 데이터를 샘플링해 실루엣 계수를 평가하는 방안을 고민해야 합니다.
평균 이동
평균 이동은 k-평균과 유사하지만, 군집 중심점(Centroid)을 데이터가 모여 있는 밀도가 가장 높은 곳으로 이동시킵니다. 평균 이동 군집화는 데이터의 분포도를 이용해 군집 중심점을 찾습니다. 이를 위해 확률 밀도 함수(probability density function)를 이용합니다. 가장 집중적으로 데이터가 모여있는 확률 밀도 함수가 피크인 점을 군집 중심점으로 선정합니다. 주어진 모델의 확률 밀도 함수를 찾기 위해 KDE(Kernel Density Estimation)를 이용합니다.
특정 데이터(군집 중심점, Centroid)를 반경 내의 확률 밀도가 가장 높은 곳으로 이동하기 위해 주변 데이터와의 거리값을 KDE 함수로 측정하고, 현재 위치를 업데이트 하며 이동합니다.
KDE(Kernel Density Estimation)는 커널(Kernel) 함수를 관측 데이터에 적용한 값을 모두 더한 뒤 데이터 건수로 나눠 확률 밀도 함수(PDF)를 추정합니다. 확률 밀도 함수는 정규분포 함수를 포함해 감마 분포, t-분포 등이 있습니다. 확률 밀도 함수를 알면 특정 변수가 어떤 값을 갖게 될지에 대한 확률을 알 수 있고 이를 통해 분산, 평균, 확률 분포 등을 알 수 있습니다.
KDE는 개별 관측 데이터(아래 그림의 빨간 점)에 커널 함수(아래 그림에선 가우시안 분포 함수)를 적용한 뒤, 이 적용 값을 모두 더한 후 개별 관측 데이터의 건수(여기선 5)로 나눠 확률 밀도 함수(오른쪽 아래 그림)를 측정하게 됩니다.

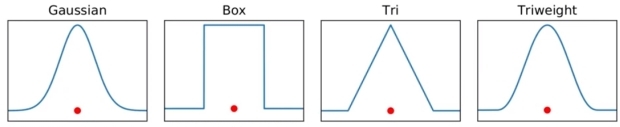
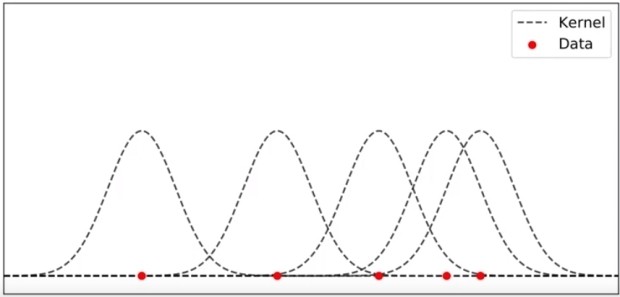

KDE는 다음과 같은 커널 함수식으로 표현됩니다. K는 커널 함수, x는 확률 변수값, xi는 관측값, h는 대역폭(bandwitdh)입니다.
$$\frac{1}{n}\sum _{i=1}^nK_h\left(x-x_i\right)=\frac{1}{nh}\sum _{i\ =1}^nK\left(\frac{x-x_i}{h}\right)$$
대역폭 h는 KDE 형태를 부드러운 형태로 평활하는 데 적용됩니다. h가 작을 수록 뾰족하게 KDE가 그려지는데, 이는 변동성이 큰 방식으로 확률 밀도 함수를 측정해서 과적합하기 쉽습니다. 반대로 h가 클수록 너무 단순화된 방식으로 확률 밀도 함수를 추정하므로 과소적홥하기 쉽습니다.
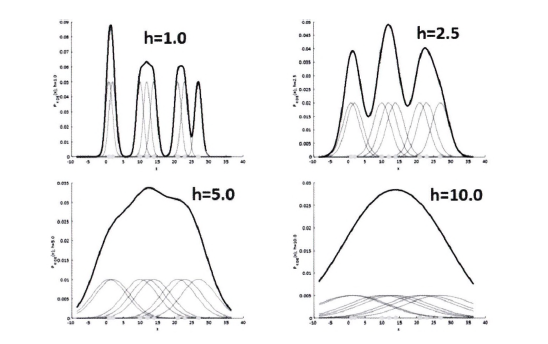
일반적으로 평균 이동 군집화는 대역폭이 클수록 단순한(평평한) KDE로 인해 적은 수의 군집 중심점을 가지게 됩니다. 반대로 대역폭이 크면 보다 많은 군집 중심점(위 그림의 뾰족한 부분)을 갖게 됩니다. 또한, 평균 이동 군집화는 군집의 개수를 지정하지 않고, 대역폭의 크기에 따라 군집화를 수행합니다.
사이킷런은 평균 이동 군집화를 위해 MeanShift 클래스를 제공합니다. MeanShift의 가장 중요한 초기화 파라미터는 bandwith입니다. 대역폭의 크기 설정이 군집화의 품질에 큰 영향을 미치기 때문에 사이킷런은 최적의 대역폭 계산을 위해 estimate_bandwitdh()함수를 제공합니다.
MeanShift & MeanShift.fit_predict()
make_blobs()을 통해 예제를 만들고 MeanShift 클래스를 적용해보겠습니다.
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import MeanShift
X, y = make_blobs(n_samples=200, n_features=2, centers=3, cluster_std=0.7, random_state=0)
meanshift = MeanShift(bandwidth=0.8)
cluster_labels = meanshift.fit_predict(X)
print('cluster labels 유형:', np.unique(cluster_labels))
'''
cluster labels 유형: [0 1 2 3 4 5]
'''군집이 6개로 분류됐습니다. 지나치게 세분화되어 과적합됨을 알 수 있습니다. bandwidth를 1.0으로 높여보겠습니다.
meanshift = MeanShift(bandwidth=1.0)
cluster_labels = meanshift.fit_predict(X)
print('cluster labels 유형:', np.unique(cluster_labels))
'''
cluster labels 유형: [0 1 2]
'''3개의 군집으로 잘 군집화됐습니다. 위에서 보았듯이 bandwidth는 군집화 개수에 큰 영향을 미칠 수 있습니다. 사이킷런은 최적화된 bandwidth를 찾기 위해 estimate_bandwidth()함수를 제공합니다.
sklearn.cluster.estimate_bandwidth
from sklearn.cluster import estimate_bandwidth
bandwidth = estimate_bandwidth(X)
print('bandwidth 값:', round(bandwidth, 3))
'''
bandwidth 값: 1.816
'''최적화된 bandwidth를 평균 이동 입력값으로 적용해 make_blobs()로 만들었던 데이터 세트에 군집화를 수행해보겠습니다.
# estimate_bandwidth()로 최적의 bandwidth 계산
best_bandwidth = estimate_bandwidth(X)
meanshift = MeanShift(bandwidth = best_bandwidth)
cluster_labels = meanshift.fit_predict(X)
print('cluster labels 유형:', np.unique(cluster_labels))
'''
cluster labels 유형: [0 1 2]
'''3개의 군집으로 잘 구성됨을 알 수 있습니다. 구성된 3개의 군집을 시각화해보겠습니다. 평균 이동도 K-평균과 유사하게 중심을 가지고 있으므로 cluster_centers_ 속성으로 군집 중심 좌표를 표시할 수 있습니다.
MeanShift.cluster_centers_
import pandas as pd
import matplotlib.pyplot as plt
clusterDF = pd.DataFrame(data=X, columns=['ftr1', 'ftr2'])
clusterDF['target'] = y
clusterDF['meanshift_label'] = cluster_labels
centers= meanshift.cluster_centers_
unique_labels = np.unique(cluster_labels)
markers=['o', 's', '^', 'x', '*']
for label in unique_labels:
label_cluster = clusterDF[clusterDF['meanshift_label']==label]
center_x_y = centers[label]
# 군집 별로 다른 마커로 산점도 적용
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], edgecolor='k',\
marker=markers[label])
# 군집 별 중심 표현
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=200, color='yellow', alpha=0.9,\
marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k', edgecolor='k',\
marker='$%d$' % label)
plt.show()
'''
결과4
'''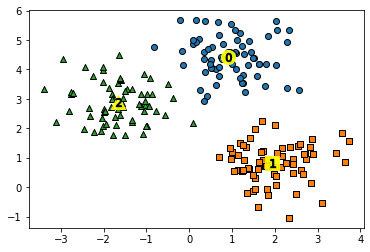
target 값과 군집 label 값을 비교해보겠습니다.
print(clusterDF.groupby('target')['meanshift_label'].value_counts())
'''
target meanshift_label
0 0 67
1 1 67
2 2 66
Name: meanshift_label, dtype: int64
'''Target 값과 군집 label 값이 1:1로 아주 잘 매칭됐습니다.
평균 이동의 장점은 데이터 세트의 형태를 특정 형태로 가정한다던가, 특정 분포도 기반의 모델로 가정하지 않기 때문에 좀 더 유연한 군집화가 가능한 것 같습니다. 또한, 이상치의 영향력도 크지 않으며, 미리 군집의 개수를 정할 필요도 없습니다. 하지만 무엇보다 알고리즘 수행 시간이 오래 걸리고, band-width의 크기에 따라 군집화 영향도가 매우 큽니다.
이러한 특징 때문에 평균 이동 군집화 기법은 분석 업무 기반의 데이터 세트보다는 컴퓨터 비전 영역에서 더 많이 사용됩니다. 이미지나 영상 데이터에서 특정 개체를 구분하거나 움직임을 추적하는 데 뛰어난 역할을 수행하는 알고리즘입니다.
GMM(Gaussian Mixture Model)
GMM은 데이터를 여러개의 가우시안 분포(정규 분포)가 섞인 것으로 간주합니다. 섞인 데이터 분포에서 개별 유형의 가우시안 분포를 추출합니다. 먼저 개별적인 3개의 가우시안 분포 A, B, C를 가진 데이터 세트가 있다고 가정해봅시다. 그렇다면 군집화를 수행하려는 실제 데이터는 아래 그림들과 같을 것입니다.
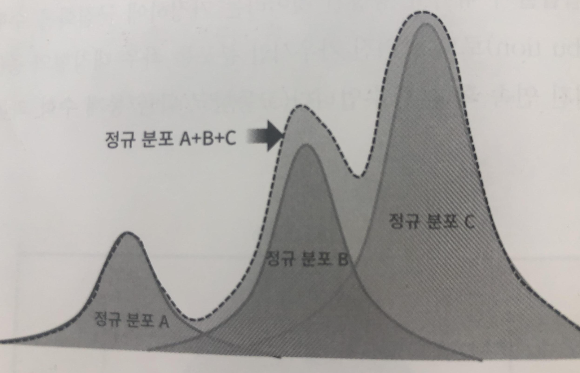

전체 데이터 세트는 서로 다른 정규 분포 A, B, C 등 여러 가지 확률 분포 곡선으로 구성될 수 있으며, 이러한 서로 다른 정규 분포에 기반해 군집화를 수행하는 것이 GMM 군집화 방식입니다.
가령 1000개의 데이터 세트가 있다면 이를 구성하는 여러 개의 정규 분포 곡선을 추출하고, 개별 데이터가 이 중 어떤 정규 분포에 속하는지 결정하는 방식입니다. 이와 같은 방식을 GMM에서는 모수 추정이라고 하는데, 모수 추정은 대표적으로 2가지를 추정하는 것입니다.
- 개별 정규 분포의 평균과 분산
- 각 데이터가 어떤 정규 분포에 해당 되는지의 확률
이러한 모수 추정을 위해 GMM은 EM(Expectation and Maximization) 방법을 적용합니다. 사이킷런은 이러한 GMM의 EM 방식을 통한 모수 추정 군집화를 지원하기 위해 GaussianMixture 클래스를 지원합니다.
GMM을 이용한 붓꽃 데이터 세트 군집화
GMM은 확률 기반 군집화이고, K-평균은 거리 기반 군집화입니다. 붗꽃 데이터 세트로 이 두가지 방식을 이용해 군집화를 수행한 뒤 결과를 비교해보겠습니다.
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
iris = load_iris()
feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
# 좀 더 편리한 데이터 Handling을 위해 DataFrame으로 변환
irisDF = pd.DataFrame(data=iris.data ,columns = feature_names)
irisDF['target'] = iris.target
sklearn.mixture.GaussianMixture & GaussianMixture.fit() & GaussianMixture.predict()
GaussianMixture의 n_components 파라미터는 K-평균의 n_clusters와 같이 군집의 개수를 정하는 데 중요한 역할을 합니다.
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=3, random_state=0).fit(iris.data)
gmm_cluster_labels = gmm.predict(iris.data)
# 군집화 결과를 irisDF의 'gmm_cluster' 칼럼 명으로 저장
irisDF['gmm_cluster'] = gmm_cluster_labels
# target 값에 따라 gmm_cluster 값이 어떻게 매핑됐는지 확인.
iris_result = irisDF.groupby(['target'])['gmm_cluster'].value_counts()
print(iris_result)
'''
target gmm_cluster
0 0 50
1 2 45
1 5
2 1 50
Name: gmm_cluster, dtype: int64
'''대부분 다 잘 매핑이 됐는데, targrt 1만 어느 정도 오류가 있었습니다. 하지만, 앞절의 k-평균 보다 효과적인 분류 결과가 도출됐습니다. k-평균 군집화를 수행한 결과를 보겠습니다.
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=0).fit(iris.data)
kmeans_cluster_labels = kmeans.predict(iris.data)
irisDF['kmeans_cluster'] = kmeans_cluster_labels
iris_result = irisDF.groupby(['target'])['kmeans_cluster'].value_counts()
print(iris_result)
'''
target kmeans_cluster
0 1 50
1 0 48
2 2
2 2 36
0 14
Name: kmeans_cluster, dtype: int64
'''이는 GMM이 k-평균보다 뛰어난 알고리즘이 아니라 붓꽃 데이터 세트에서 군집화에 더 효과적이라는 뜻입니다. k-평균 데이터는 평균 거리를 중심으로 중심을 이동하면서 군집화를 수행하는 방식이므로 개별 군집 내의 데이터가 원형으로 흩어져 있는 경우 매우 효과적으로 군집화가 수행될 수 있습니다.
GMM과 K-평균의 비교
KMeans는 원형의 범위에서 군집화를 수행합니다. 데이터 세트가 원형의 범위를 가질 수록 KMeans의 군집화 효율은 더욱 높아집니다. make_blobs()의 군집의 수를 3개로 하고, cluster_std를 0.5와 같이 작게 설정하면 데이터가 원형 형태로 분산될 수 있습니다.
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=100, n_features=2, cluster_std=0.5, random_state=0)
result = KMeans(n_clusters=3, init='k-means++', max_iter=300).fit_predict(X)
features = pd.DataFrame(data=X, columns=['ftr1', 'ftr2'])
features['target'] = result
markers=['^', 's', 'o']
labels = np.unique(result)
for label in labels:
data = features[features['target']==label]
plt.scatter(x=data['ftr1'], y=data['ftr2'], marker=markers[label])
plt.show()
'''
결과1
'''
KMeans는 대표적으로 길쭉한 타원형으로 늘어선 경우 군집화를 수행하지 못합니다. 다음에 해당하는 데이터 세트를 make_blobs()의 데이터를 변환해서 만들어보겠습니다.
군집화를 시각화하는 함수 visualize_cluster_plot(clusterobj, dataframe, label_name, iscenter=True)를 만들어보겠습니다. 이 함수의 파라미터는 아래와 같습니다.
- clusterobj: 사이킷런의 군집 수행 객체, KMeans나 GuassianMixture의 fit, predict로 군집화를 완료한 객체. 군집화 결과 시각화가 아니고 make_blobs()로 생성한 데이터일 경우 None 입력
- dataframe: 피처 데이터 세트와 레이블 값을 가진 DataFrame
- label_name: 군집화 결과 시각화인 경우, dataframe 내 군집화 label 칼럼명, make_blobs() 결과 시각화일 경우 dataframe 내의 target 칼럼명
- iscenter: 사이킷런 Cluster 객체가 군집 중심 좌표를 제공하면 True, 그렇지 않으면 False
def visualize_cluster_plot(clusterobj, dataframe, label_name, iscenter=True):
if iscenter :
centers = clusterobj.cluster_centers_
unique_labels = np.unique(dataframe[label_name].values)
markers=['o', 's', '^', 'x', '*']
isNoise=False
for label in unique_labels:
label_cluster = dataframe[dataframe[label_name]==label]
if label == -1:
cluster_legend = 'Noise'
isNoise=True
else :
cluster_legend = 'Cluster '+str(label)
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], s=70,\
edgecolor='k', marker=markers[label], label=cluster_legend)
if iscenter:
center_x_y = centers[label]
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=250, color='white',
alpha=0.9, edgecolor='k', marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k',\
edgecolor='k', marker='$%d$' % label)
if isNoise:
legend_loc='upper center'
else: legend_loc='upper right'
plt.legend(loc=legend_loc)
plt.show()from sklearn.datasets import make_blobs
# make_blobs()로 300개의 데이터 세트, 3개의 군집 세트, cluster_std=0.5를 만듦
X, y = make_blobs(n_samples=300, n_features=2, centers=3, cluster_std=0.5, random_state=0)
# 길게 늘어난 타원형의 데이터 세트를 생성하기 위해 변환함.
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)
# feature 데이터 세트와 make_blobs()의 y 결과값을 DataFrame으로 저장
clusterDF = pd.DataFrame(data=X_aniso, columns=['ftr1', 'ftr2'])
clusterDF['target'] = y
# 생성된 데이터 세트를 target 별로 다른 마커로 펴시해 시각화함
visualize_cluster_plot(None, clusterDF, 'target', iscenter=False)
'''
결과2
'''
위와 같이 길쭉한 데이터 세트에서 KMeans가 어떻게 군집화를 하는지 확인해 보겠습니다.
# 3개의 군집 기반 Kmeans를 X_aniso 데이터 세트에 적용
kmeans = KMeans(3, random_state=0)
kmeans_label = kmeans.fit_predict(X_aniso)
clusterDF['kmeans_label'] = kmeans_label
visualize_cluster_plot(kmeans, clusterDF, 'kmeans_label', iscenter=True)
'''
결과3
'''
KMeans로 군집화를 수행할 경우 원형을 중심으로 영역이 군집화 됐음을 알 수 있습니다. 길쭉한 경우 KMeans의 경우 최적의 군집화가 어렵습니다.
이번엔 GMM으로 군집화를 수행해보겠습니다.
# 3개의 n_components 기반 GMM을 X_aniso 데이터 세트에 적용
gmm = GaussianMixture(n_components=3, random_state=0)
gmm_label = gmm.fit(X_aniso).predict(X_aniso)
clusterDF['gmm_label'] = gmm_label
# GaussianMixture는 cluster_centers_ 속성이 없으므로 iscenter를 False로 설정.
visualize_cluster_plot(gmm, clusterDF, 'gmm_label', iscenter=False)
'''
결과4
'''
데이터가 분포된 방향에 따라 정확하게 군집화됐음을 알 수 있습니다. GMM은 군집의 중심 좌표를 구할 수 없어 군집 중심 표현을 구하지 않습니다.
make_blobs()의 target값과 KMeans, GMM의 군집 Label 값을 서로 비교해 얼만큼 군집화 효율 차이가 발생하는지 확인해보겠습니다.
print('### KMeans Clusteing ###')
print(clusterDF.groupby('target')['kmeans_label'].value_counts())
print('\n### Gaussian Mixture Clustering ###')
print(clusterDF.groupby('target')['gmm_label'].value_counts())
'''
### KMeans Clusteing ###
target kmeans_label
0 2 73
0 27
1 1 100
2 0 86
2 14
Name: kmeans_label, dtype: int64
### Gaussian Mixture Clustering ###
target gmm_label
0 2 100
1 1 100
2 0 100
Name: gmm_label, dtype: int64
'''이처럼 GMM의 경우 KMeans보다 유연하게 다양한 데이터 세트에 잘 적용될 수 있습니다. 하지만 군집화를 위한 수행 시간이 오래 걸린다는 단점이 있습니다.
DBSCAN(Density Based Spatial Clustering of Applications with Noise)
밀도 기반 군집화의 대표적인 알고리즘은 DBSCAN에 대해 알아보겠습니다. DBSCAN은 간단하고 직관적인 알고리즘으로 돼 있음에도, 특정 공간 내에 데이터 밀도 차이를 기반 알고리즘으로 하고 있어서 복잡한 기하학적 분포도를 가진 데이터 세트에 대해서도 군집화를 잘 수행합니다.
DBSCAN을 구성하는 가장 중요한 두 가지 파라미터는 입실론(epsilon)으로 표기하는 주변 영역과 이 입실론 주변 영역에 포함되는 최소 데이터 개수 min points입니다.
- 입실론 주변 영역(epsilon): 개별 데이터를 중심으로 입실론 반경을 가지는 원형의 영역입니다.
- 최소 데이터 개수(min points): 개별 데이터의 입실론 주변 영역에 포함되는 타 데이터의 개수입니다.
입실론 주변 영역 내에 포함되는 최소 데이터 개수를 충족시키는가 아닌가에 따라 데이터 포인트를 다음과 같이 정의합니다.
- 핵심 포인트(Core Point): 주변 영역 내에 최소 데이터 개수 이상을 가진 데이터
- 이웃 포인트(Neighbor Point): 주변 영역 내에 위치한 데이터
- 경계 포인트(Border Point): 주변 영역 내에 최소 데이터 개수 미만을 가지지만, 핵심 포인트를 이웃 포인트로 가진 데이터
- 잡음 포인트(Noise Point): 주변 영역 내에 최소 데이터 개수 미만을 가지고, 핵심 포인트를 이웃포인트로 가지는 않는 데이터

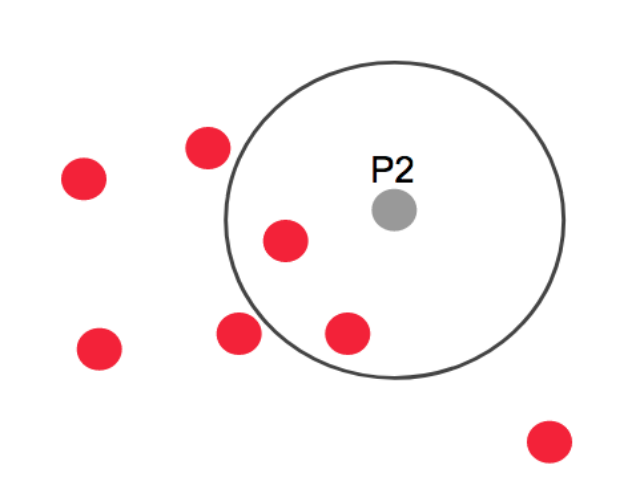

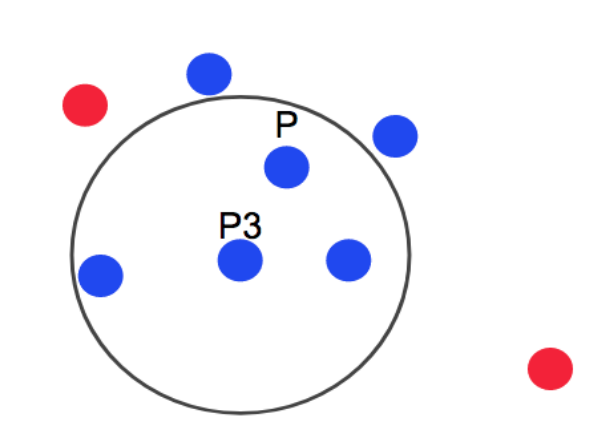

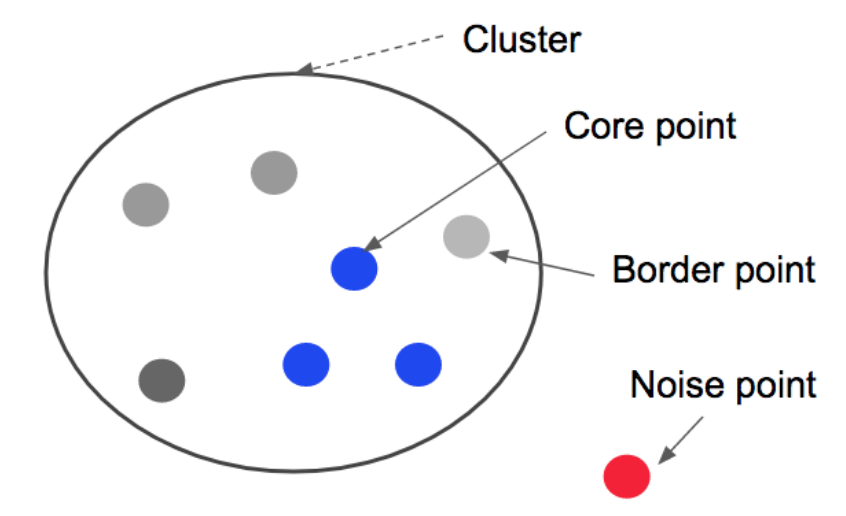
DBSCAN은 점 P에 epsilon이라는 반경의 원에 포함된 최소 데이터 개수를 만족하면 Core Point가 됩니다. 여기서 최소 데이터 개수는 3입니다. P2(Border point)의 경우 주변에 데이터가 2개 이지만, 포함된 점이 모두 Core Point라서 Border Point가 됩니다. 여기에 속하지 않는 점은 Noise Point가 되고, 클러스터의 경계는 Core Point만 서로 연결하면서 군집화를 구성합니다. 결국 군집의 끝에는 Border Point가 존재하게 됩니다.
사이킷런은 DBSCAN 클래스를 통해 DBSCAN 알고리즘을 지원합니다. DBSCAN 클래스는 다음과 같은 주요한 초기화 파라미터를 가지고 있습니다.
- eps: 입실론 주변 영역의 반경을 의미합니다.
- min_samples: 반경 내에 포함될 데이터의 최소 개수를 의미합니다.(자신 포함, 즉 min points + 1)
DBSCAN 적용하기 - 붓꽃 데이터 세트
sklearn.cluster.DBSCAN
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
iris = load_iris()
feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
irisDF = pd.DataFrame(data=iris.data, columns=feature_names)
irisDF['target'] = iris.target
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.6, min_samples=8, metric='euclidean')
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
irisDF['target'] = iris.target
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)
'''
target dbscan_cluster
0 0 49
-1 1
1 1 46
-1 4
2 1 42
-1 8
Name: dbscan_cluster, dtype: int64
'''eps는 보통 1 이하의 값을 사용합니다. dbscan_cluster 값을 보면, 0과 1외에 특이하게 -1이 군집 레이블로 있는 것을 알 수 있습니다. -1인 군집은 Noise에 속하는 군집을 의미합니다. 따라서 붓꽃 데이터 세트는 0과 1 두 개의 군집으로 군집화됐습니다.
DBSCAN은 군집의 개수를 자동으로 지정합니다. Target 값의 유형이 2개라고 해서 2개가 됐다고 군집화 효율이 떨어지는 것은 아닙니다. 오히려 붓꽃 데이터 세트는 군집을 3개로 하는 것보다 2개로 하는 것이 군집화 효율로서 더 좋은 면이 있습니다.
DBSCAN으로 군집화 데이터 세트를 2차원 평면에서 표현하기 위해 PCA를 이용해 2개의 피처로 압축 변환한 뒤 앞 예제에서 사용한 visualize_cluster_plot()함수를 이용해 시각화해보겠습니다.
from sklearn.decomposition import PCA
# 2차원으로 시각화하기 위해 PCA n_components=2로 피처 데이터 세트 변환
pca = PCA(n_components=2, random_state=0)
pca_transformed = pca.fit_transform(iris.data)
# visualize_cluster_plot()함수는 ftr1, ftr2 칼럼을 좌표에 표현하므로
# PCA 변환값을 해당 칼럼으로 생성
irisDF['ftr1'] = pca_transformed[:, 0]
irisDF['ftr2'] = pca_transformed[:, 1]
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)
'''
결과1
'''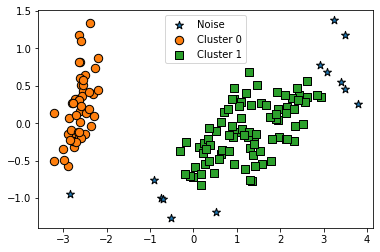
PCA로 2차원으로 표현하니 이상치 노이즈 데이터가 명확히 드러납니다. DBSCAN을 적용할 때는 특정 군집 개수로 군집을 강제하지 않는 것이 좋습니다. DBSCAN 알고리즘에 적절한 eps와 min_samples 파라미터를 통해 최적의 군집을 찾는 것이 중요합니다.
eps를 증가시키면 반경이 커져서 노이즈 데이터가 작아집니다. min_samples가 커지면 더 많은 데이터가 반경에 들어가야 core point로 인식하기 때문에, 노이즈 데이터 개수가 많아집니다.
eps를 0.6에서 0.8로 증가시키면 노이즈 데이터 수가 줄어듭니다. 예제로 확인해보겠습니다.
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.8, min_samples=8, metric='euclidean')
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
irisDF['target'] = iris.target
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)
'''
target dbscan_cluster
0 0 50
1 1 50
2 1 47
-1 3
Name: dbscan_cluster, dtype: int64
'''
'''
결과2
'''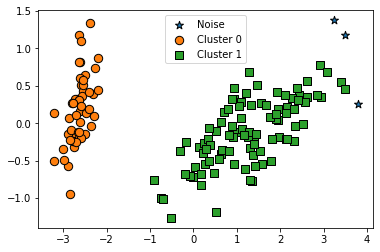
노이즈 군집인 -1이 3개 밖에 없습니다. 기존 eps가 0.6일 때 노이즈로 분류된 데이터가 eps 반경이 커지면서 Cluster 1에 소속됐습니다. 이번엔 min_samples 값만 16으로 변경해보겠습니다.
dbscan = DBSCAN(eps=0.6, min_samples=16, metric='euclidean')
'''
target dbscan_cluster
0 0 48
-1 2
1 1 44
-1 6
2 1 36
-1 14
Name: dbscan_cluster, dtype: int64
'''
'''
결과3
'''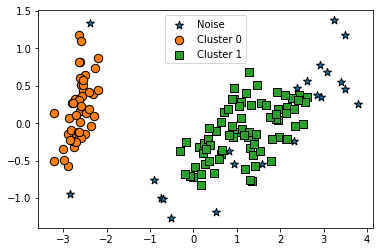
노이즈 데이터가 많아짐을 알 수 있습니다.
DBSCAN 적용하기 - make_circles() 데이터 세트
이번에는 복잡한 기하학적 분포를 가지는 데이터 세트에서 DBSCAN과 타 알고리즘을 비교해보겠습니다. 먼저 make_circles() 함수를 이용해 원 형태로 돼있는 2차원 데이터 세트를 만들겠습니다. make_circles() 함수는 오직 2개의 피처만 생성하므로 별도의 피처 개수를 지정할 필요가 없습니다.
파라미터 noise는 노이즈 데이터 세트의 비율, factor는 외부 원과 내부 원의 scale 비율입니다.
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000, shuffle=True, noise=0.05, random_state=0, factor=0.5)
clusterDF = pd.DataFrame(data=X, columns=['ftr1', 'ftr2'])
clusterDF['target'] = y
visualize_cluster_plot(None, clusterDF, 'target', iscenter=False)
'''
결과4
'''
make_circles()는 내부 원과 외부 원으로 구별되는 데이터를 생성함을 알 수 있습니다. 먼저, K-평균과 GMM은 어떻게 군집화 하는지 보겠습니다.
KMeans
# KMeans로 make_circles()데이터 세트를 군집화 수행.
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, max_iter=1000, random_state=0)
kmeans_labels = kmeans.fit_predict(X)
clusterDF['kmeans_cluster'] = kmeans_labels
visualize_cluster_plot(kmeans, clusterDF, 'kmeans_cluster', iscenter=True)
'''
결과5
'''
군집 중심을 위와 아래 절반으로 군집화했습니다. 거리 기반 군집화는 위와 같이 특정한 형태로 지속해서 이어지는 부분을 찾아내기 어렵습니다.
GMM
# GMM으로 make_circles() 데이터 세트를 군집화 수행.
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=2, random_state=0)
gmm_label = gmm.fit(X).predict(X)
clusterDF['gmm_cluster'] = gmm_label
visualize_cluster_plot(gmm, clusterDF, 'gmm_cluster', iscenter=False)
'''
결과6
'''
GMM은 일렬로 늘어선 데이터 세트에서는 효과적으로 군집화 적용이 가능했으나, 원형으로 구성된 복잡한 데이터 세트에서는 군집화가 원하는 방향으로 되지 않았습니다. 이제 DBSCAN으로 군집화를 적용해보겠습니다.
# DBSCAN으로 make_circles() 데이터 세트 군집화 수행.
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.2, min_samples=10, metric='euclidean')
dbscan_labels = dbscan.fit_predict(X)
clusterDF['dbscan_cluster'] = dbscan_labels
visualize_cluster_plot(dbscan, clusterDF, 'dbscan_cluster', iscenter=False)
'''
결과7
'''
DBSCAN으로 정확히 원하는 방향으로 군집화가 됐음을 알 수 있습니다.
정리
이번 장에서는 머신러닝 기반의 군집화 기법을 소개했습니다. 각 군집화 기법은 나름의 장/단점을 가지고 있으며, 데이터의 특성에 맞게 선택해야 합니다.
k-평균은 거리 기반으로 군집 중심점을 이동시키면서 군집화를 수행합니다. 쉽고 직관적인 알고리즘이라 많이 애용되지만, 복잡한 구조를 가지는 데이터 세트에 적용하기에 한계가 있으며, 군집의 개수를 최적화하기 어렵습니다. 이를 평가하기 위해 실루엣 계수를 이용합니다.
평균 이동(Mean Shift)는 k - 평균과 유사하지만, 군집 중심점이 각 군집의 데이터 밀도가 가장 높은 쪽으로 이동하며 군집화를 수행합니다. 컴퓨터 비전 영역에서 이미지, 영상 속 특정 개체를 구분하는 데 뛰어난 역할을 합니다.
GMM은 군집화를 적용하고자 하는 데이터가 여러 가우시안 분포가 더해진 확률 분포로 가정해 군집화를 수행하는 방식입니다. GMM의 경우 다양한 데이터 세트에 잘 적용될 수 있지만, 수행 시간이 오래 걸린다는 단점이 있습니다.
DBSCAN은 밀도 기반 군집화의 대표적인 알고리즘이며, 데이터 포인트를 분류해 직접 접근이 가능한 다른 핵심 포인트를 서로 연결하며 군집화를 구성하는 방식입니다. DBSCAN은 간단하고 직관적인 알고리즘이지만, 기하학적으로 복잡한 데이터 분포에도 효과적인 군집화가 가능합니다.
궁금한 점
- cluster_centers_: 각 군집 중심점 좌표(Shape는 [군집 개수, 피처 개수]): 왜 col 갯수는 피처 개수인가? 피처가 축의 개수, x, y 축이 있으면 그 좌표를 줘야 해서 col이 피처 개수이다.
- iris_result = irisDF.groupby(['target', 'cluster'])['sepal_length'].count()에서 왜 sepal_length인가?는 iris_result2 = irisDF.groupby(['target', 'cluster']).count()의 결과가 아래와 같고, 경우의 수에 맞춰 피처의 개수를 세어주기 때문이다.
# iris_result2의 결과
'''
sepal_length sepal_width petal_length petal_width
target cluster
0 1 50 50 50 50
1 0 48 48 48 48
2 2 2 2 2
2 0 14 14 14 14
2 36 36 36 36
'''- 이는 cluster 0과 2의 경우 피처의 위치 자체가 명확히 분리되기 어려운 부분이 존재합니다가 무슨 말이지? 0, 2번 군집의 데이터 위치가 붙어 있는 위치라는 뜻
- 여러 개의 클래스에 해당하는 데이터 세트를 만드는데, 하나의 클래스에 여러 개의 군집이 분포될 수 있게 데이터를 생성할 수 있습니다가 무슨 말이지?
- DataFrame.groupby()는 GroupBy() 오브젝트를 반환하는데, 뒤에 메서드를 쓰면서 통계를 낸다. DataFrame과는 다른 객체인 것 같다. groupby()['columns']에서 ()괄호 안의 값을 기준으로 []의 columns의 값을 새던가 평균을 내던가 등을 할 수 있다.
- KDE의 확률 변수 x가 뭘 말하는 거지? xi는 뭐고?
- GMM 여러 개의 정규 분포 곡선을 추출하는 방법은? EM인데, 찾아봐야한다.
- 각 군집의 데이터의 확률 분포가 정규 분포를 이룬다는 가정을 한 후 출발한다.
- 각 군집의 모수(평균, 분산)를 임의로 추측한 후 클러스터링을 한 뒤, 이를 기반으로 예측한 군집을 이용해 다시 모수를 추정하는 과정을 반복한다. 아직, E-STEP 수식을 이해하지 못했다. (뒷부분)
- https://angeloyeo.github.io/2021/02/08/GMM_and_EM.html
출처: 파이썬 머신러닝 완벽 가이드(권철민)
사진 출처:
https://kurt7191.tistory.com/50
https://yenaworldblog.wordpress.com/2019/01/08/kernel-density-estimation-kde-%EC%9D%B4%ED%95%B4/
https://ariz1623.tistory.com/224
http://ai4school.org/?page_id=3685
Ⅳ.자료와 학습(중급) – 5. K-평균 알고리즘 – AI4School
추측컨대 그룹1은 주로 업무시간대에 사용이 몰려 있는 것으로 보아 업무용 메신저일 것입니다. 밤에는 사용자가 낮보다 현저히 적네요. 이제부터 그룹1은 [타라그래] 메신저로 명명하죠. 그
ai4school.org
'파이썬 머신 러닝 완벽 가이드' 카테고리의 다른 글
| 텍스트 분석 (0) | 2021.12.03 |
|---|---|
| 군집화 실습 - 고객 세그먼테이션 (0) | 2021.12.02 |
| 차원 축소 (0) | 2021.11.26 |
| 회귀 실습 - 캐글 주택 가격: 고급 회귀 기법 (0) | 2021.11.24 |
| 회귀 실습 - 자전거 대여 수요 예측 (0) | 2021.11.23 |